Chapter 9 Measures of Central Tendency
A measure of central tendency is a way of talking about the common values from a set of data points. In this section, we’ll talk about two: the mean and the median.
9.1 The Mean and mean()
The most common measure of central tendency is the average, which is often referred to as the mean. Sometimes, you’ll see it represented as the greek letter mu \(\left( \mu \right)\), or as \(\bar{x}\). If we have a set of numbers – let’s say those numbers are 0, 5, -5, 10, -10, 40, and 100 – we compute the average as follows:
\[ \bar{x} = \frac{0 + 5 + \left( -5 \right) + 10 + \left( -10 \right) + 40 + 100}{7} = \frac{140}{7} = 20 \]
This may seem trivial, so let’s get to the fun part of doing it in R. First thing is first: we need our numbers to get loaded into R. Aha! A perfect time for a vector. Since we called the average \(\bar{x}\), let’s name this vector x.
Now we need to go and actually calculate \(\bar{x}\). Well we’re calculating the mean, so we should try the mean() function.
## [1] 20This returns (gives back) the mean of x, and we can see that it is, in fact, 20. Another way that we could have done this is more like we would have done by hand: first we would have to sum the numbers, then we’d have to divide them by the number of numbers we just added together. Luckily, the sum() and length() functions save us a lot of time and energy.
## [1] 20Again, we get that the average is 20, thus both methods are valid.
Handling NA Values
What would happen in functions like mean(), sum(), length(), min(), or max() when NAs are present? Well let’s find out. We’ve inserted a few NAs into the same vector as above, but we’ve called it y now so as not to confuse the two.
## [1] NA## [1] NAThey return NA! You may be asking yourself, why? Well, the reason this happens is because you haven’t told R how to deal with a non-existent value (We told you they’d be pesky!). You most likely want R to ignore the NA altogether, so we can take advantage of an argument called na.rm and set it equal to TRUE.
## [1] 20## [1] 140Great, everything is working again! Problem solved.
mean() with TRUE/FALSE
It’s also good to note that R can take the mean of logical vectors. What happens is that TRUE is coerced to be 1, and FALSE is coerced to be 0. Then, the mean is taken just as before. This may seem boring, but it allows us to determine percentages quickly. Let’s say we want to find the percentage of students that responded to Survey 1 that maintained at least a 3.0 GPA. How would we figure this out if we were doing it by hand? Probably like this:
- Get an observation of data (that is, go to the first response)
- Check the GPA for that responder
- If the GPA is 3.0 or higher, we add 1 to our tally
- Otherwise, add 0
- After going through all observations, take the final tally and divide by the number of observations we observed (that had values)
Luckily, there’s a very good way to do this in R, and it involves the mean() function. In addition to evaluating the mean of a vector of numbers, it can compute the percentage of observations that meet a certain condition, given by something called a conditional statement. We talked about them before, so now it’s time to see why we spent the time learning how to write them. We’ll show the “complete” version of the process we just outlined, and then we’ll go through and do it the short way.
# Create TRUE/FALSE vector of places where students have GPAs above 3.0
bool_vec = survey1$GPA > 3.0
head(bool_vec)## [1] TRUE TRUE TRUE TRUE FALSE FALSE# Coerce the TRUE/FALSE vector to be 1s and 0s
bool_as_binary = as.numeric(bool_vec)
head(bool_as_binary)## [1] 1 1 1 1 0 0## [1] 0.7800983This works, but there’s a faster way to do it. We can see that the last step of summing and dividing by the length is the same as the mean() function, so we can just change that to be mean(bool_as_binary) and get the same result. But bool_as_binary is just the numeric coersions of bool_vec, and R knows to do this coersion automatically when using a function like mean() on a vector of type logical. So it’s equally valid to say mean(bool_vec), although we’ll take it one step farther. We’ll put the conditional statement that created bool_vec directly into the mean() function, and we should get the same result.
## [1] 0.7800983Not only did we save four lines of code to get the same result, but we saved a little memory (storage space) in the process. This is because we didn’t need to store the result of the conditional or its coersion as vectors to be used later. R just handled it all internally. This exact procedure is very useful when you want to check how much data is above a threshhold in a quick way.
9.2 The Median and median()
The median, or middle number, is the other most common measure of central tendency. It’s the point in which our data gets split in half. To determine the median by hand, we’d follow the following process:
- Arrange data in numerical order from smallest to greatest
- Cross off the two endpoints
- Move in one data point from each end of the range of data
- Repeat steps 2 and 3 until either:
- One number remains in the middle, or
- Two numbers remain in the middle
- If one number remains, we’ve found our median. If two numbers remain, take the mean of the last two remaining data points.
Let’s find the median of this list of numbers:
By hand, we’d put them in the following order:
Then we’d cross them off, endpoint pair by endpoint pair, until we reach the middle:
We’re down to two numbers, so we just take the average of the remaining numbers, which are 6 and 10. We get 8, so this is our median.
As was the case with mean(), R comes with a great function – the median() function – to calculate the median of a list of numbers. We can supply the vector directly to median() and immediately get the median.
## [1] 8Skewed Histograms
Sometimes, you’ll get data that’s heavily skewed one way or another. This means that the mean and the median are not in the same place. Let’s take a quick look:
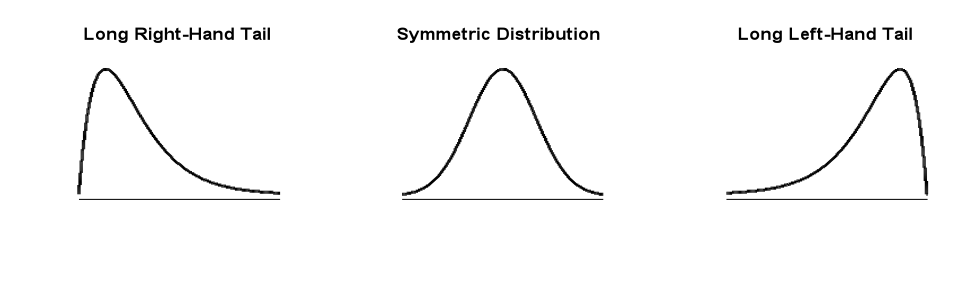
Figure 9.1: Skewed and Symmetric Distributions
The plot on the left shows a histogram that’s right-skewed. This means that the mean is greater than \(\left( \gt \right)\) the median.
The middle plot shows a symmetric distribution. This means that the mean is equal to the median.
The plot on the right shows a histogram that’s left-skewed. This means that the mean is less than \(\left( \lt \right)\) the median.
9.3 Standard Deviation and sd()
Lastly, we should talk about the standard deviation. This is how spread out around our average the data is. The standard deviation applies to the whole vector, not just an individual point. We’ll talk about how to use the concept of a standard deviation for just a single data point in the next chapter.
Breaking the term down, we can understand a little bit more intuitively what exactly a standard deviation is. A deviation is how far a particular point is from another point (in our case, the average), and standard typically means the average, or divided by how many points there are. So really, a standard deviation is a way to look at the average difference of any data point from the average of the data. Note: The standard deviation can never be negative, since it doesn’t make sense to be a negative distance from the average.
The standard deviation is calculated as
\[ \sqrt{\frac{1}{n} \sum_{i = 1}^n \left( x_i - \bar{x} \right)^2} \]
Now that the scary math is out of the way, let’s make it make sense. We’ll define a process to calculate the standard deviation, and rebuild that equation as we go.
- Calculate the average, \(\bar{x}\), of all of the data points
- Take each point in the data, which we’ll call \(x_i\) (think of \(i\) as the \(i^{th}\) element of the vector of data points), and subtract off the average. These are the deviations
- Pro tip: These deviations should always add to 0
- Square the difference in step 2. Mathematically, we’ve got \[\left( x_i - \bar{x} \right)^2\]
- Take the average of the squared differences in step 3. That’s where the \(\frac{1}{n} \sum_{i = 1}^n\) comes from, and it gives us what’s called the variance, and it’s a single number: \[ \frac{1}{n} \sum_{i = 1}^n \left( x_i - \bar{x} \right)^2 \]
- Take the square root of the variance we just found in step 4. This is the standard deviation, and it’s given by \[ \sqrt{\frac{1}{n} \sum_{i = 1}^n \left( x_i - \bar{x} \right)^2} \]
We’ll do a quick example as a table with this list of numbers:
.
The average of the list is 3.
| \(x_i\) | \(x_i - \bar{x}\) | \(\left( x_i - \bar{x} \right)^2\) |
|---|---|---|
| 0 | -3 | 9 |
| 1 | -2 | 4 |
| 2 | -1 | 1 |
| 3 | 0 | 0 |
| 4 | 1 | 1 |
| 5 | 2 | 4 |
| 6 | 3 | 9 |
We then average the last column to get 4, and take the square root to get a standard deviation of 2.
Now that we see how the process works and can do it by hand, we’re ready to use the R function sd() to speed the process along. Just pass the vector of values to sd() and the standard deviation will be computed.
## [1] 2.160247
Hmmm… That’s not quite right. By hand, we got 2, but with sd(), we got 2.1602469. This is where we need to start being a little careful. Earlier, we defined standard deviation as the standard deviation of the population (frequently referred to as \(\sigma\)), which is given by
\[ \sigma = \sqrt{\frac{1}{n} \sum_{i = 1}^n \left(x_i - \bar{x} \right)^2} \]
However, in R, the sd() function computes the sample standard deviation, which is slightly different. (We’ll cover it later on in the class, but to help you understand what R is doing, we need to introduce the difference now.) The sample standard deviation, \(s\), is given by
\[ s = \sqrt{\frac{1}{n-1} \sum_{i = 1}^n \left(x_i - \bar{x} \right)^2} \]
The the sd() function is actually computing \(s\) and not \(\sigma\). That’s okay though! A quick bit of algebra helps us to make the conversion between the sample and the population.

To get from \(s\) to \(\sigma\), we just need to multiply by \(\sqrt{\frac{n - 1}{n}}\). The \(n - 1\) in the numerator cancels the \(n - 1\) in the denominator of \(s\), and then the \(n\) in the denominator is the \(n\) in \(\sigma\). So, to get the population standard deviation, we need to do this:
## [1] 2All fixed! Let’s put this into a function so that we can do it on any data set we’d like. We’ll call the function stdv(), which takes one argument (the numeric vector x), and returns the population standard deviation.
The larger the standard deviation is, the more spread out our data is. The smaller the standard deviation, the less spread the deviation is. As an extreme case, a standard deviation of 0 means that there is no spread whatsoever. This is because all of the data would be located at the average.
9.4 Mean and Standard Deviation After Changing The Data
The mean and median change if we add, subtract, multiply, or divide the same number to every point in our data. They will change by the exact amount that we’ve added or subtracted (i.e. if we add 4 to every number, the average and median increase by 4. Dividing by 12 will divide the average and median by 12).
The standard deviation changes differently under addition, subtraction, multiplication, and division. Addition and subtraction don’t have any impact on the standard deviation, while multiplication and division change the standard deviation by the same value (i.e. if we multiply every point by 6, the standard deviation is multiplied by 6 as well) If the factor that the data points are multiplied by is negative, the standard deviation is multiplied/divided by the absolute value of the factor.
Note: We don’t immediately know how the average, median, or standard deviation change by doing any of these operations to just a single point in our data, but R makes these computations easy.